[UE5 C++] 절차적 랜덤 맵 그래프 생성하기 (최소신장트리 알고리즘)
발단
다니던 부트캠프의 최종 프로젝트를 진행하는 중 랜덤 맵 그래프를 구현해야 할 일이 생겼다. 따라서 구현 내용을 정리하고자 한다. 구현은 게임인스턴스의 서브시스템인 DungeonGenerateSystem에 하였다.

위 그래프는 던전 입장 시마다 랜덤하게 생성된다.
그래프의 레퍼런스는 스팀의 Shape of Dreams 라는 게임을 레퍼런스로 했다.

1. 노드 생성
노드는 전투, 보상, 보스 노드로 이루어져 있다.
DungeonNode & DungeonGraph 구조체
사용자에게 보여지는 그래프의 형태가 이쁘게 보이는 것이 중요하다 생각했다. 따라서 노드마다 FVector2D(2D 공간의 좌표) 를 가지고 있도록 했다.
UENUM(BlueprintType)
enum class ENodeType : uint8
{
Battle,
Reward,
Boss
};
USTRUCT(BlueprintType)
struct FDungeonNode
{
GENERATED_BODY()
UPROPERTY(BlueprintReadWrite)
int32 NodeID;
UPROPERTY(BlueprintReadWrite)
int32 AssignedMapID;
UPROPERTY(BlueprintReadWrite)
ENodeType NodeType;
UPROPERTY(BlueprintReadWrite)
FVector2D UICoordinate;
UPROPERTY(BlueprintReadWrite)
TArray<int32> ConnectedNodeIDs;
};
USTRUCT(BlueprintType)
struct FDungeonGraph
{
GENERATED_BODY()
UPROPERTY(BlueprintReadWrite)
TArray<FDungeonNode> Nodes;
UPROPERTY(BlueprintReadWrite)
TArray<FVector2D> BezierPoints;
UPROPERTY(BlueprintReadWrite)
int32 StartNodeID = -1;
UPROPERTY(BlueprintReadWrite)
int32 BossNodeID = -1;
};
항상 랜덤성을 부여할 때 C언어에서도 널리 쓰이던 Rand 함수를 UE5에서도 제공한다. 차이점이 있다면 시드를 설정하지 않아도 매번 랜덤하게 값을 생성할 수 있다는 점이다.
80프로 확률로 전투 노드가 생성되고, 각각 10프로 확률로 보상, 보스 노드들이 생성된다. 보스 노드는 최소 1개를 보장하기 위해 마지막 노드 생성 시에도 보스 노드가 없다면 생성하도록 했다.
// Determine Map`s Type
float Prob = FMath::RandRange(0.0f,100.f);
// First, Check is there any boss room in DungeonGraph
if (CurrentNotAssignedNodeNum == MaxNodeNum - 1 && DungeonGraph.BossNodeID == -1)
{
// Boss
FDungeonNode NewNode = MakeNewNode(CurrentNotAssignedNodeNum,0,ENodeType::Boss, CandidatePoint);
DungeonGraph.Nodes.Add(NewNode);
DungeonGraph.BossNodeID = CurrentNotAssignedNodeNum;
CurrentNotAssignedNodeNum++;
}
else if (Prob > 0.0f && Prob < 80.f)
{
// Battle 1~5 Map Assign
float RandNum = FMath::RandRange(1,5);
FDungeonNode NewNode = MakeNewNode(CurrentNotAssignedNodeNum,RandNum,ENodeType::Battle, CandidatePoint);
DungeonGraph.Nodes.Add(NewNode);
CurrentNotAssignedNodeNum++;
}
else if (Prob >= 80.f && Prob < 90.f)
{
// Reward
FDungeonNode NewNode = MakeNewNode(CurrentNotAssignedNodeNum,0,ENodeType::Reward, CandidatePoint);
DungeonGraph.Nodes.Add(NewNode);
CurrentNotAssignedNodeNum++;
}
else if (Prob >= 90.f && Prob < 100.f)
{
// Boss
bool HasBossRoom = false;
for (auto iter : DungeonGraph.Nodes)
{
if (iter.NodeType == ENodeType::Boss)
{
HasBossRoom = true;
break;
}
}
if (HasBossRoom)
{
continue;
}
FDungeonNode NewNode = MakeNewNode(CurrentNotAssignedNodeNum,0,ENodeType::Boss, CandidatePoint);
DungeonGraph.Nodes.Add(NewNode);
DungeonGraph.BossNodeID = CurrentNotAssignedNodeNum;
CurrentNotAssignedNodeNum++;
}
}
2. 최소 신장 트리 연결 (Kruskal, Union-Find 알고리즘 사용)
노드를 만들었으니 간선을 연결해야 할 것이다. 우선 나의 시행착오는 아래와 같다.
시행착오 (더보기 클릭)
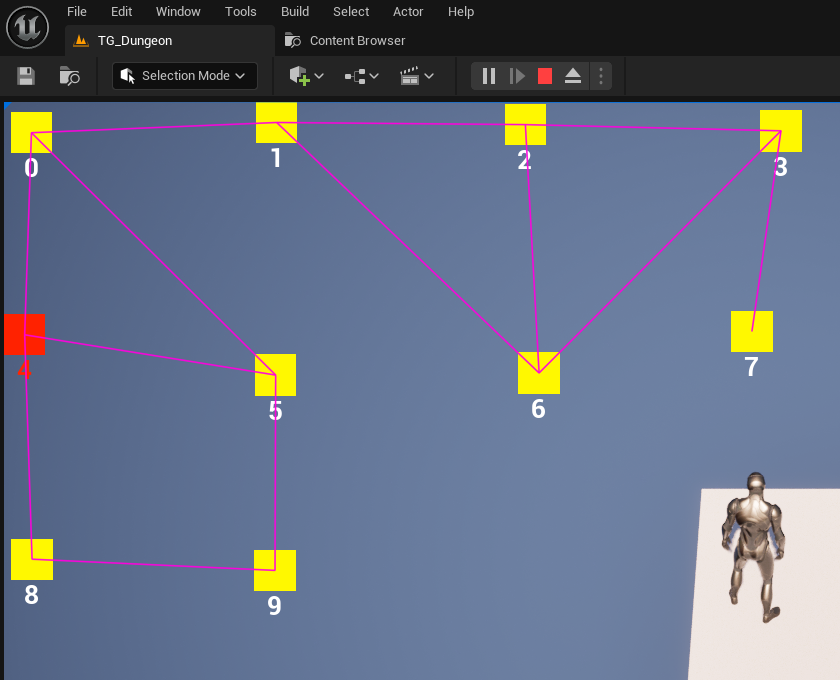
처음에는 특별한 알고리즘 없이 위와 같은 그래프를 생성하려고 시도했었다. 구현이 처음이다 보니 레퍼런스를 충분히 분석하지 않고 구현을 시도했었고, 결과적으로 아래와 같은 그래프를 생성하게 되었다.
노드의 간선 연결은 거리를 기반으로 하였다.
for (int i = 0 ; i < 10 ; i++)
{
const int32 Columns = 4;
const float GridX = 300.f;
const float GridY = 250.f;
const float OffsetX = 40.f;
const float OffsetY = 30.f;
// 위치 설정
int32 Row = i / Columns;
int32 Col = i % Columns;
FVector2D BasePosition = FVector2D(Col * GridX, Row * GridY);
FVector2D RandomOffset = FVector2D(FMath::FRandRange(-OffsetX, OffsetX), FMath::FRandRange(-OffsetY, OffsetY));
위와 같은 방식으로 생성하려 했지만, 정말 비효율적임을 시각화로 뼈져리게 느낄 수 있었다.
따라서 기존 방식을 뒤엎고 다시 만들어보기로 했다.
시행착오 끝
위에 서술한 시행착오를 기반으로, 기존 방식을 뒤엎고 다시 레퍼런스를 분석해 보았다.


분석 결과 레퍼런스 이미지들이 대부분 곡선을 그리고 있다는 점을 알게 되었고, 곡선을 기준으로 랜덤한 위치에 노드들을 생성하면 위 레퍼런스처럼 보이지 않을까? 라는 생각을 했다.
따라서 아래와 같은 순서를 따라 구현을 시도했다.
- 베지어 곡선을 랜덤 방식이 아니라 고정된 Points 들을 통해 그려본다.
- 그려진 곡선 주위로 노드를 랜덤 생성해본다.
- 최소신장트리 알고리즘을 활용하여 모든 노드들이 연결되도록 한다.
- 인접한 노드들끼리 간선으로 잇는다.
- 완성?
여기서 베지어 곡선이란?
시작, 끝, 컨트롤 포인트를 통해 곡선을 표현할 수 있는 방법.
베지에 곡선 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 2차 베지어 곡선 3차 베지어 곡선 베지에 곡선 혹은 베지어 곡선(Bézier Curve)은 n {\displaystyle n} 개의 점으로부터 얻어지는 n − 1 {\displaystyle n-1} 차 곡선으로 수치
ko.wikipedia.org
StartPoint, EndPoint, ControlPoint 정의
bool UMJDungeonGenerationSubSystem::GenerateDungeonGraph()
{
UMJGameInstanceTG* MJGI = Cast<UMJGameInstanceTG>(GetGameInstance());
uint8 MaxNodeNum = MJGI->GetMaxNodeNum();
FVector2D StartPoint;
FVector2D EndPoint;
FVector2D ControlPoint;
uint8 CurrentNotAssignedNodeNum = 0;
FVector2D ViewportSize = FVector2D(1920.f,1080.f);
// Sets Bezier Curve Points (for now, just one curve)
StartPoint = FVector2D(ViewportSize.X / 4,ViewportSize.Y * 0.5);
EndPoint = FVector2D(ViewportSize.X - ViewportSize.X / 4,ViewportSize.Y * 0.5);
ControlPoint = FVector2D(ViewportSize.X/2,ViewportSize.Y * 0.05);
베지에 곡선 방정식 함수
FVector2D UMJDungeonGenerationSubSystem::GetQuadBezier(float t, const FVector2D StartPoint, const FVector2D EndPoint,
const FVector2D ControlPoint)
{
return pow((1-t),2) * StartPoint + 2 * (1-t) * t * ControlPoint + pow(t,2) * EndPoint;
}
위 두 코드를 통해 While문에서
while (CurrentNotAssignedNodeNum < MaxNodeNum)
{
// divide curve and make nodes
float t = static_cast<float>(CurrentNotAssignedNodeNum) / (MaxNodeNum - 1);
FVector2D BezierPoint = GetQuadBezier(t, StartPoint, EndPoint, ControlPoint);
DungeonGraph.BezierPoints.Add(BezierPoint);
이런 방식으로 곡선을
곡선의 길이 / 노드 개수 로 나누어서 곡선의 일정 위치마다 노드를 생성하게 했다. (t는 0~1까지의 변화량)
생성 결과

베지어 포인트를 DungeonGraph 에 추가해 OnPaint 함수에서 Draw Lines 하였다.
3. 인접 간선 연결
이제 노드마다 간선을 연결할 차례이다. 시행착오 에서 서술했듯이 거리별로 노드를 이어주는 것은 아름다운 결과를 만들지는 못 했다. 레퍼런스를 분석하니 두 가지 조건을 만족함을 알 수 있었다.
- 모든 노드들은 순회 가능할 것.
- 인접 노드로는 무조건 이동 가능할 것.
1번 조건에서는 최소 신장 트리를 만들어야 함을 알 수 있었고, 2번 조건을 통해 결국에는 물리적 거리를 통해 간선을 한 번 더 이어줘야 함을 알 수 있었다.
따라서 두 가지 알고리즘을 활용했다.
Kruskal 알고리즘
모든 노드들을 사이클을 형성하지 않고 최소 비용으로 연결하는 알고리즘
Union-Find 알고리즘
여러 개의 노드 집합이 존재할 때, 각 집합들이 서로 같은 집합인지 판별하는 알고리즘
익히 알려져 있는 알고리즘이므로 해당 알고리즘에 대한 자세한 설명은 아래 레퍼런스 블로그를 참조하길 바란다.
레퍼런스
최소 스패닝 트리 (MST) : 크루스칼 알고리즘 (Kruskal Algorithm)
최소 스패닝 트리 (MST, Minimum Spanning Tree) 그래프의 스패닝 트리(신장 트리, Spanning Tree)란, 그래프의 모든 정점을 잇지만 사이클이 없는 부분 그래프를 의미한다. 위와 같은 그래프에서, 양쪽의 붉
4legs-study.tistory.com
[알고리즘] Union-Find 알고리즘
서로소 집합(Disjoint-Set) 알고리즘이라고도 불리는 알고리즘으로 구체적으로 여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 노드가 서로 같은 그래프에 속하는지 판별하는 알고
velog.io
[언리얼 엔진] TTuple
Unreal Engine TTuple 개요 언리얼 엔진에서 TTuple을 사용하려 하는데 공식 가이드 문서도 없고(API 페이지만 있음) 마땅한 참고 예제가 없어 정리하고자 한다. Tuple은 2개이상의 값을 하나의 변수에 담
wecandev.tistory.com
두 알고리즘을 통해 노드들을 연결한 것을 확인할 수 있다.

소스 코드 (ConnectNodesMyMST)
void UMJDungeonGenerationSubSystem::ConnectNodesByMST(float MaxDistance)
{
const uint8 NodeCount = DungeonGraph.Nodes.Num();
if ( NodeCount <= 1 ) return;
// make tuple for candidateEdges
TArray<TTuple<uint8, uint8, float>> AllCandidateEdges;
for (int i = 0 ; i< NodeCount ; i++)
{
for (int j = 0 ; j < NodeCount ; j++)
{
if (i == j) continue;
float Distance = FVector2D::Distance(DungeonGraph.Nodes[i].UICoordinate,DungeonGraph.Nodes[j].UICoordinate);
AllCandidateEdges.Add(MakeTuple(i,j,Distance));
}
}
// 2. sort by ascend
AllCandidateEdges.Sort([](const TTuple<uint8, uint8, float>& A, const TTuple<uint8, uint8, float>& B)
{
return A.Get<2>() < B.Get<2>();
});
// 3. create Parent Array for union find & lamda functions
TArray<int16> Parent;
Parent.Init(-1,NodeCount);
std::function<uint8(uint8)> Find = [&Parent, &Find](uint8 Node) -> uint8
{
if (Parent[Node] < 0 ) return Node;
return Parent[Node] = Find(Parent[Node]);
};
std::function<bool(uint8, uint8)> Union = [&Parent, &Find](uint8 A, uint8 B) -> bool
{
uint8 RootA = Find(A);
uint8 RootB = Find(B);
if (RootA == RootB) return false;
Parent[RootB] = RootA;
return true;
};
// 4. choose edge based on union find
for (const auto& iter : AllCandidateEdges)
{
uint8 NodeA = iter.Get<0>();
uint8 NodeB = iter.Get<1>();
if (Union(NodeA, NodeB))
{
DungeonGraph.Nodes[NodeA].ConnectedNodeIDs.Add(NodeB);
DungeonGraph.Nodes[NodeB].ConnectedNodeIDs.Add(NodeA);
}
}
// 5. All the nodes and edges are visualized in UMG Widget
}
이제 최소 연결(순회 가능) 을 보장했으니 인접 노드끼리 연결해 주면 된다.
GenerateDungeonGraph 함수의 끝단에서 최소신장트리 연결, 물리적 인접 노드 연결을 실행했다.
GenerateDungeonGraph 중
// Choose most far node from BossNode
float MaxDist = FLT_MIN;
uint8 MaxDistNodeNum = -1;
for (auto& iter : DungeonGraph.Nodes)
{
if (iter.NodeType != ENodeType::Battle)
continue;
if (MaxDist < FVector2D::Distance(DungeonGraph.Nodes[iter.NodeID].UICoordinate, DungeonGraph.Nodes[DungeonGraph.BossNodeID].UICoordinate))
{
MaxDist = FVector2D::Distance(DungeonGraph.Nodes[iter.NodeID].UICoordinate, DungeonGraph.Nodes[DungeonGraph.BossNodeID].UICoordinate);
MaxDistNodeNum = iter.NodeID;
}
}
DungeonGraph.StartNodeID = MaxDistNodeNum;
SavedMapNodeNum = DungeonGraph.StartNodeID;
ConnectNodesByMST(FVector2D::Distance(FVector2D(0.0f,0.0f), ViewportSize)); // 최소신장트리 연결
ConnectNodesByDistance(400.f,4); // 물리적 근접 노드 연결
return true;
}
총평
결과적으로 위 과정들을 통해

레퍼런스와 비슷하게 맵 그래프를 랜덤으로 생성할 수 있었다. 현재 위치한 노드에서 인접한 노드들로만 UI 를 클릭해 이동할 수 있다. 시스템 테스트 과정으로 UI 는 Image 와 DrawLine 함수를 이용하여 임시 구현한 것이므로 후에 UI 기획이 확정되면 다시 글을 수정하겠습니다.
2025.06.20 현재 UI 관련해 서술하지 않는 이유
- 임시 구현이기도 하고, 무엇보다 블루프린트가 가득함..


현재는 한 개의 베지에 곡선을 사용하여 맵이 생성되지만, 후에 여러 커브들을 추가해 더 많은 무작위한 맵 생성을 적용해 볼 예정이다.